Question

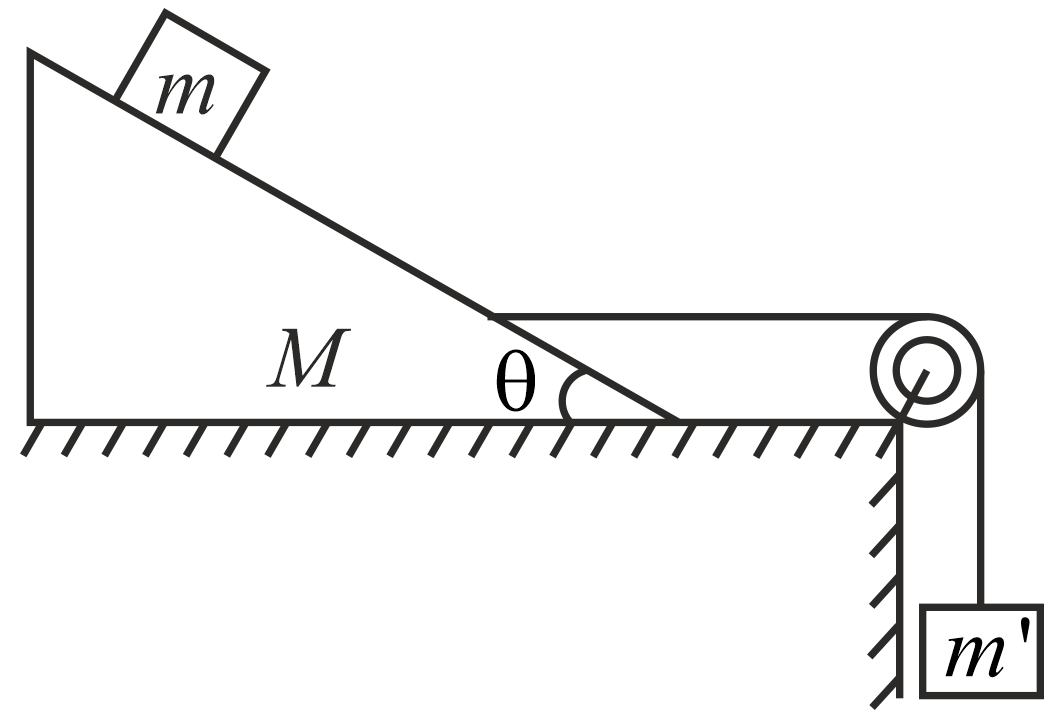
A hanging block of mass $m^{'}$ prevents the smaller block of mass $m$ from slipping over a movable triangular block of mass $M$ . All the surfaces are frictionless and the strings and the pulleys are light. Value of mass $m^{'}$ in terms of $m$ , $M$ and $\theta $ is

• A. $\left[\frac{m + M}{\cot \theta - 1}\right]$
• B. $\left[\frac{m - M}{\cot \theta + 1}\right]$
• C. $\left[\frac{m - M}{\cot \theta - 2}\right]$
• D. $\left[\frac{m + M}{\cot \theta + 2}\right]$

Answer 1

Answer: (A)

Pulling force is $m^{\prime} g$, while mass in motion is $m+M+m^{\prime}$. So acceleration of the system will be given by $a =\frac{( m )^{\prime} g }{\left( m + M +( m )^{\prime}\right)} \ldots . .$ (i)
Mass $m$ will not slide over $M$ if
$a \cos \theta=g \sin \theta$....(ii)
From equation (i) in (ii), we get
$\frac{( m )^{\prime} g \cos \theta}{\left( m + M +( m )^{\prime}\right)}= g \sin \theta \operatorname{or}( m )^{\prime}=\left[\frac{ m + M }{\cot \theta-1}\right]$