Q.
A half spherical glass lens with refractive index $1.5$ is placed in a liquid with refractive index of $1.3$ (see following figure). The radius of the half spherical lens is $10\, cm$. A parallel beam of light travelling in the liquid is refracted by the glass lens. Then the absolute value of the position of the image from the centre of the glass lens will be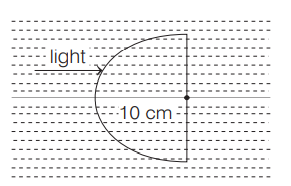
TS EAMCET 2018
Solution: