Question

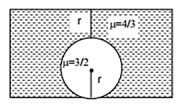
A glass sphere having refractive index $\left(3 / 2\right)$ is having a small irregularity at its centre. It is placed in a liquid of refractive index $\frac{4}{3}$ such that the surface of the liquid is at a distance $r$ above the sphere, where $r=20 \, cm$ is radius of the sphere. If the irregularity is viewed from above then what is it's distance (in $cm$ ) from the centre where eye will observe the irregularity?

Answer 1

Consideration refraction at glass-water interface.
$\frac{\mu _{2}}{v}-\frac{\mu _{1}}{u}=\frac{\mu _{2} - \mu _{1}}{R}$
$\Rightarrow \, \, \frac{4}{3 v}-\frac{3}{- 2 r}=\frac{\left(4 / 3\right) - \left(3 / 2\right)}{r}$

$\Rightarrow \, \frac{4}{3 v}+\frac{3}{2 r}=-\frac{1}{6 r}$
$\therefore \, \, \, v=\frac{r}{5}$
Now refraction at water air surface
$u=-\left(r + \frac{4}{5} r\right)=-\frac{9 r}{5}$
$\frac{\mu _{2}}{v}-\frac{\mu _{1}}{u}=\frac{\mu _{2} - \mu _{1}}{\infty}$
$\Rightarrow \frac{1}{v}+\frac{4 \times 5}{3 \times 9 r}=\frac{1 - \left(4 / 3\right)}{\infty}$
$\frac{1}{v}=-\frac{20}{27 r}$
$v=-\frac{27 r}{20}$
So height above center $=2r-\frac{27 r}{20}$
$=\frac{40 r - 27 r}{20}=\frac{13}{20}r=13cm$