Question

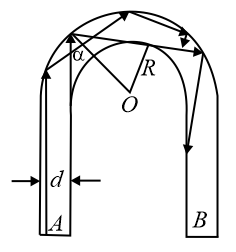
A glass rod of rectangular cross-section is bent into the shape shown in the diagram. A parallel beam of light falls perpendicularly on the flat surface $A$ . Determine the minimum value of the ratio $\frac{R}{d}$ for which all light entering the glass through surface $A$ will emerge from the glass through surface $B$ . The index of refraction of the glass is $1.5$ .

Answer 1

Consider the representative rays shown in diagram. A ray entering the glass through surface $A$ and passing along the inner side of the rod will be reflected by the outer side with the smallest angle $\alpha $ , at which the reflected ray is tangent to the inner side. We have to consider the conditions under which the ray will undergo total internal reflection before reaching $B$ .

If $\alpha > \theta _{\text{c}}$ , the critical angle, at which total internal reflection occurs, all the incident beam will emerge through the surface $B$ . Hence, we require
$\text{sin} \alpha > \frac{1}{\text{n}}$
The geometry gives $\text{sin} \alpha = \frac{\text{R}}{\left(\text{R} + \text{d}\right)}$
Therefore $\frac{R}{R + d}\geq \frac{1}{n}$ ,
or $\left(\frac{R}{d}\right)_{m i n}=\frac{1}{n - 1}=\frac{1}{1 .5 - 1}=2$