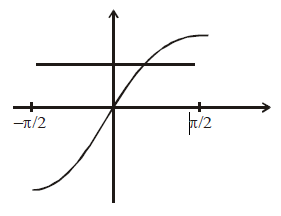Q. A function $f : R \to [-1, 1]$ defined by $f(x) = \sin \, x, \forall x \, \in \, R$, where R is the subset of real numbers is one-one and onto if R is the interval:
Relations and Functions - Part 2
Solution:
We know that f (x) is said to be one-one
If $f (x_1) = f (x_2) \, \Rightarrow \, x_1= x_2$
f (x) is said to be onto if f (x) is always increasing.
$\therefore \, x \in \left[- \frac{\pi}{2} , \frac{\pi}{2} \right] \, \, \, (\because \, f (x) = \sin \, x)$