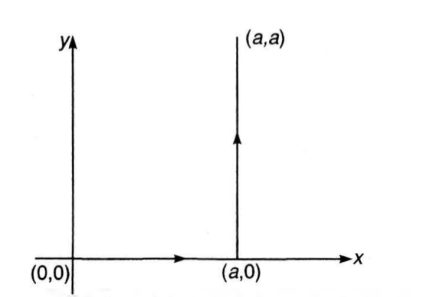
Question

A force $ F = - k (y \hat{i}+ x\hat{j}) $(where A: is a positive constant) acts on a particle moving in the $x-y$ plane. Starting from the origin, the particle is taken along the positive x-axis to the point $(a,0)$ and then parallel to the y-axis to the point $(a,a )$. The total work done by the force $F$ on the particle is

• A. $ -2ka^2$
• B. $ 2ka^2$
• C. $ -ka^2$
• D. $ ka^2$

Answer 1

Answer: (C)

$d W= F \cdot d s$, where $d s =d x \hat{ i }+d y \hat{ j }+d z \hat{ k }$
and $F =-k(y \hat{ i }+x \hat{ j })$
$\therefore d W=-k(y d x+x d y)=-k d(x y)$
$\therefore W=\int\limits_{0,0}^{a, a} d W=-k \int\limits_{0,0}^{a, a} d(x y)$
$=-k[x y]_{0,0}^{a, a}$
$W=-k a^{2}$
Alternate Answer
While moving from $(0,0)$ to $(a, 0)$ along positive $x$-axis,

$y=0 \therefore F =-k x \hat{ j }$ i.e. force is in negative $y$-direction while the displacement is in positive $x$-direction. Therefore, $W_{1}=0$ (Force $\perp$ displacement).
Then, it moves from $(a, 0)$ to $(a, a)$ along a line parallel to $y$-axis $(x=+a)$. During this $F =-k(y \hat{ i }+a \hat{ j })$
The first component of force, $-k y \hat{ i }$ will not contribute any work, because this component is along negative $x$-direction $(-\hat{ i })$ while displacement is in positive $y$-direction $(a, 0)$ to $(a, a)$
The second component of force i.e. $-k a \hat{j}$ will perform
negative work $\begin{bmatrix} F _{y}=-k a \hat{ j } \\ s =a \hat{ j }\end{bmatrix}, W_{2}=(-k a)(a)=-k a^{2}$
$\therefore W=W_{1}+W_{2}=-k a^{2}$