Question

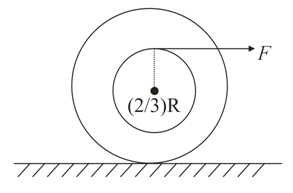
A force $F=12\,μmg$ acts tangentially at the given point of the disc which is at a distance of $\frac{2}{3}R$ from centre of disc as shown in figure. Disc is kept on a rough horizontal plane of coefficient of friction $\mu $ . The angular acceleration of the disc is (mass of the disc is $m$ and its radius is $R$ )

• A. $\frac{40 \mu g}{3 R}$
• B. $\frac{18 \mu g}{R}$
• C. $\frac{20 \mu g}{3 R}$
• D. $\frac{14 \mu g}{R}$

Answer 1

Answer: (D)

$r=\frac{I_{c m}}{m R}=\frac{m R^{2}}{m R}=\frac{R}{2}$
But force acts above to it so friction on the disc acts along the applied force. Torque about centre of mass $\frac{m R^{2} \alpha }{2}=12\mu mg\left(\frac{2}{3} R\right)-\mu mgR=7\mu mgR$
$\alpha =\frac{14 \mu g}{R}$