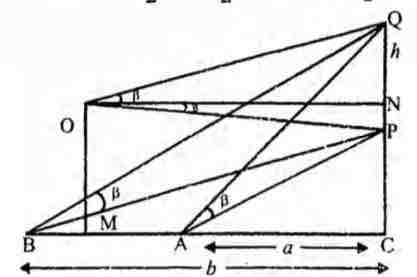
Q. A flagstaff on the top of a house subtends the same angle P at two points distance a and b from the house and on the same side of it, then the length of flagstaff is.
Solution:
Let PQ be the length of the flagstaff on the top P of the house OP. Let $\Delta$QBP = $ \beta , \, \Delta$QAP = $\beta$. Let O be the centre of the circle through A, B, P, Q. Let M be the mid-point of AB and N be the midpoint of PQ. From $\Delta$ONQ, tan $\beta = \frac{NQ}{ON} $ or NQ = ON tan $\beta$ NQ = CM tan $\beta$ Also BM = $\frac{1}{2} $ AB = $\frac{1}{2} $ (BA - AC) = $\frac{1}{2} (b - a)$ QN = (CA + AM) tan $\beta$ = $(CA + MB) $ tan $\beta$ = $\left( a + \frac{b- a}{2} \right) $ tan $\beta = \frac{a +b}{2}$ tan $\beta$ $\therefore $ PQ = 2NQ = $(a + b)$ tan $\beta$