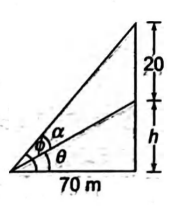
Q. A flagstaff $20\, m$ high standing on the top of a house subtends an angle whose tangent is $1 / 6$ at a distance $70\, m$ from the foot of the house. The height of the house is
Trigonometric Functions
Solution:
$\tan \alpha=\tan (\phi-\theta) \tan \alpha$
$\Rightarrow \frac{1}{6}=\frac{\frac{20+h}{70}-\frac{h}{70}}{1+\frac{(20+h) h}{(70)^{2}}}$
$\Rightarrow(70)^{2}+20 h+h^{2}=(6)(70)(20)$
$\Rightarrow h^{2}+20 h+70(70-120)=0$
$\Rightarrow h^{2}+20 h-(50)(70)=0$
$\Rightarrow h=\frac{-20 \pm \sqrt{400+(4)(50)(70)}}{2}=50\, m$