1. Tardigrade
  2. Question
  3. Mathematics
  4. A flagpole stands on a building of height 450 ft and an observer on a level ground is 300 ft from the base of the building. The angle of elevation of the bottom of the flagpole is 30° and the height of the flagpole is 50 ft. If θ is the angle of elevation of the top of the flagpole, then tan θ is equal to

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

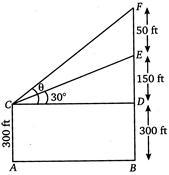
Q. A flagpole stands on a building of height $450\, ft$ and an observer on a level ground is $300 \,ft$ from the base of the building. The angle of elevation of the bottom of the flagpole is $ 30{}^\circ $ and the height of the flagpole is $50\, ft$. If $ \theta $ is the angle of elevation of the top of the flagpole, then $ \tan \theta $ is equal to

KEAMKEAM 2008Trigonometric Functions

Solution:

In $ \Delta DCE, $
$ \tan 30{}^\circ =\frac{150}{CD}\Rightarrow CD=\frac{150}{1/\sqrt{3}} $
$ \Rightarrow $ $ CD=\sqrt{3}\times 150 $
Now, in $ \Delta DCF, $ $ \tan \theta =\frac{DF}{CD}=\frac{200}{\sqrt{3}.150}=\frac{4}{3\sqrt{3}} $

Solution Image