Q.
A disk of radius $R$ and mass $M$ is at equilibrium at position $D$ on the smooth inclined plane which makes an angle $\theta$ with the vertical as shown. The disk's centre is attracted to a point A located at a vertical distance d above the surface as shown. Assume that the force of attraction is proportional to the distance from the disk's centre of mass to point $A$, i.e. assume that $F =- kr$, where $r$ is the distance from the point A to the disk's centre of mass and $k$ is constant. Then, distance $BD$ is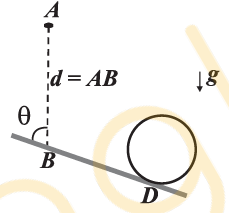
UPSEEUPSEE 2018
Solution:
