Q.
A disk of radius $a/4$ having a uniformly distributed charge $6 C$ is placed in the $x - y$ plane with its centre at $(-a / 2,0,0)$. A rod of length 'a' carrying a uniformly distributed charge $8 \,C$ is placed on the $x$-axis from $x=a / 4$ to $x=5 a / 4$. Two point charges $-7\, C$ and $3\, C$ are placed at $(a / 4,-a / 4,0)$ and $(-3 \,a / 4,3 \,a / 4,0)$, respectively. Consider a cubical surface formed by six surfaces $x=\pm a / 2, y=\pm a / 2, z=\pm a / 2$. The electric flux through this cubical surface is: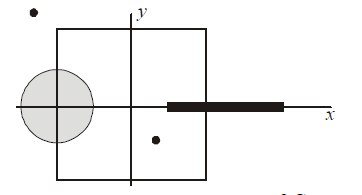
BITSATBITSAT 2017
Solution: