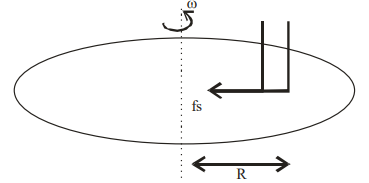
Question

A disc with a flat small bottom beaker placed on it at a distance $R$ from its center is revolving about an axis passing through the center and perpendicular to its plane with an angular velocity $\omega$. The coefficient of static friction between the bottom of the beaker and the surface of the disc is $\mu$. The beaker will revolve with the disc if :

• A. $R \leq \frac{\mu g }{2 \omega^{2}}$
• B. $R \leq \frac{\mu g }{\omega^{2}}$
• C. $R \geq \frac{\mu g }{2 \omega^{2}}$
• D. $R \geq \frac{\mu g }{\omega^{2}}$

Answer 1

Answer: (B)

For beaker to move with disc

$f_{s}=m \omega^{2} R$
We know that $f _{ s } \leq f _{ s \max }$
$m \omega^{2} R \leq \mu m g$
$R \leq \frac{\mu g }{\omega^{2}}$