Q.
A disc (of radius $r cm$ ) of uniform thickness and uniform density $\sigma$ has
a square hole with sides of length $l=\frac{r}{\sqrt{2}} cm .$ One corner of the hole is located at the centre of the disc and centre of the hole lies on $y$ -axis as shown. Then the $y$ -coordinate of position of centre of mass of disc with hole (in $cm$ ) is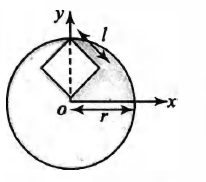
System of Particles and Rotational Motion
Solution: