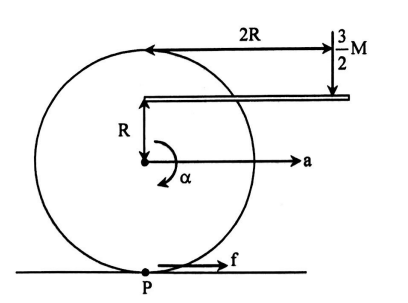
Q.
A disc of mass $M$ & radius $R$ is placed a rough horizontal surface with its axis horizontal. A light rod of length '$2R$' is fixed to the disc at point '$A$' as shown in figure and a force $\frac{3}{2} M g$ is applied at the other end. If disc starts to roll without slipping find the value of " $10 \times \mu_{\min } "$ where $\mu_{\min }$ is minimum coefficient of friction $b / w$ disc & horizontal surface required for pure rolling-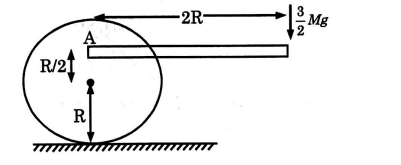
System of Particles and Rotational Motion
Solution: