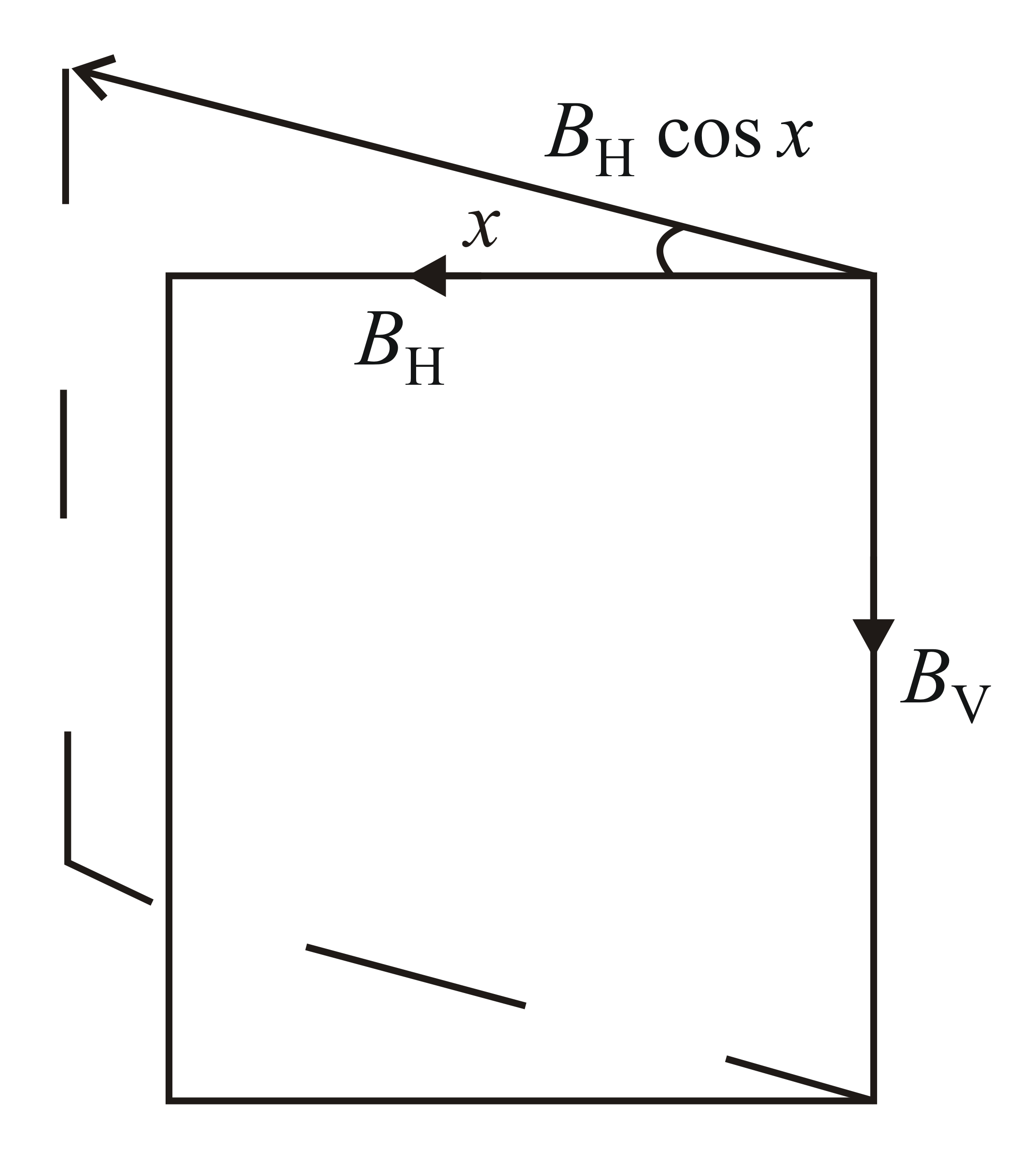
Question

A dip needle lies initially in the magnetic meridian when it shows an angle of $\operatorname{dip} \theta$ at a place. The dip circle is rotated through an angle $x$ in the horizontal plane and then it shows an angle of $\operatorname{dip} \theta^{\prime}$. Then what is the value of $\frac{\tan \theta^{\prime}}{\tan \theta} ?$

• A. $\frac{1}{\cos x}$
• B. $\frac{1}{\sin x}$
• C. $\frac{1}{\tan x}$
• D. $\cos x$

Answer 1

Answer: (A)

In first case $\tan \theta=\frac{B_{ V }}{B_{ H }} \ldots \ldots \ldots \ldots(i)$
In second case, when the needle is rotated at an angle $x$ with the magnetic meridian, the horizontal component of earth's
magnetic field $B_{ H } \cos x$ will be responsible for the orientation of the $\text{dip}$ needle. $\tan \theta^{\prime}$
$=\frac{B_{ V }}{B_{ H } \cos x} \ldots \ldots \ldots$ (ii)
Dividing equation (ii) by equation (i)
$\frac{\tan \theta^{\prime}}{\tan \theta}=\frac{1}{\cos x}$