Q.
A differentiable function $f(x)$ satisfying integral equation $f(x)=\left(\log _c x\right)^2-\int\limits_1^e \frac{f(t)}{t} d t$. Suppose $f(x)+\frac{1}{6}=g(x)$.
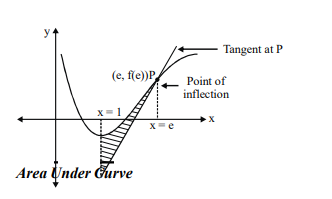
The area of the region bounded by the tangent line of $y=f(x)$ at the point $(e, f(e))$, the curve $y$ $=f(x)$ and the line $x=1$ is equal to
Application of Integrals
Solution:
$f ( x )=(\ln x )^2-\frac{1}{6} $
$f ^{\prime}( x )=\frac{2 \ln x }{ x }>0 \quad \text { for } x \in(1, e ) $
$y =\frac{2 x }{ e }-\frac{7}{6}$
$A =\int\limits_1^{ e }\left((\ln x )^2-\frac{1}{6}\right)-\left(\frac{2 x }{ e }-\frac{7}{6}\right) dx $
$ A = e +\frac{1}{ e }-3$