Q. A dietician wishes to mix together two kinds of food $X$ and $Y$ in such a way that the mixture contains atleast $10$ units of vitamin $A, 12$ units of vitamin $B$ and $8$ units of vitamin $C$. The vitamin content of $1\, kg$ food is given below
J & K CETJ & K CET 2013Linear Programming
Solution:
From the given data, we get the following LPP Min $ Z=16x+20y $ S.t. $ x+2y\ge 10, $ $ 2x+2y\ge 12 $ $ 3x+y\ge 8 $ and $ x\ge 0,\,\,y\ge 0 $ First we assume all the inequalities as equations
Equations
Points
$ x+2y=0 $
$ (0,\,5) $ and $ (10,\,0) $
s $ 2x+2y=12 $
$ (0,6) $ and $ (6,0) $
$ 3x+y=8 $
$ (0,8) $ and $ \left( \frac{8}{3},0 \right) $
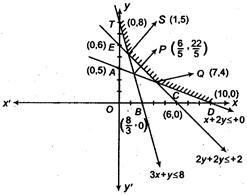
Now, we plot all these points on graph paper for getting a convex region.
For intersection point P, $ \begin{align} & x+2y=10 \\ & 6x+12y=16 \\ & -\,\,\,\,\,\,\,\,\,\,-\,\,\,\,\,\,\,\,\,\,\,- \\ & \_\_\_\_\_\_\_\_\_\_\_ \\ & -5x=-6 \\ \end{align} $ $ \Rightarrow $ $ x=\frac{6}{5} $ and they $ y=\frac{22}{5} $ $ \therefore $ Convex region is TSQD with extreme point $ T(0,8),\,S(1,5),\,Q(2,\,4) $ and $ D(10,0). $ Now, apply coner point method
Points
Objective function $ \min \,\,z=16x+20y $
$ T(0,\,8) $
$ 16\times 0+20\times 8=160 $
$ S(1,\,5) $
$ 16\times 1+20\times 5=116 $
$ Q(2,\,4) $
$ 16\times 2+20\times 4=112 $ (min)
$ D(10,\,0) $
$ 16\times 10+20\times 0=160 $
So, the least cost of the mixture is Rs. 112.