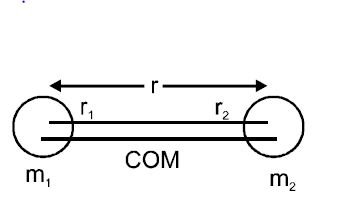
Q. A diatomic molecule is made of two masses $m_1$ and $m_2$ which are separated by a distance $r$. If we calculate its rotational energy by applying Bohr's rule of angular momentum quantization, its energy will be given by : ($n$ is an integer)
AIEEEAIEEE 2012Atoms
Solution:
$m_{1}r_{1}=m_{2}r_{2}$
$r_{1}+r_{2}=r$
$\therefore r_{1}=\frac{m_{2}r}{m_{1}+m_{2}}$
$r_{2}=\frac{m_{2}r}{m_{1}+m_{2}}$
$\therefore \varepsilon=\frac{1}{2}I\omega^{2}$
$=\frac{1}{2}\left(m_{1}r^{2}_{1}+m_{2}r_{2}^{2}\right).\omega^{2} ............\left(i\right)$
$mvr=\frac{h}{2\pi}=I\omega$
$\omega=\frac{nh}{2\pi I}
\,\varepsilon = \frac{1}{2}I. \frac{n^{2}h^{2}}{4\pi^{2}I^{2}}$
$=\frac{n^{2}h^{2}}{8\pi ^{2}} \frac{1}{\left(m_{1}r^{2}_{1}+m_{2}r^{2}_{2}\right)}$
$=\frac{n^{2}h^{2}}{8\pi ^{2}} \frac{1}{m_{1} \frac{m^{2}_{2}r^{2}_{0}}{\left(m_{1}+m_{2}\right)^{2}} }+m_{2} \frac{m^{2}_{1}r^{2}}{\left(m_{1}+m_{2}\right)^{2}}$
$=\frac{n^{2}h^{2}}{8\pi^{2}r^{2}} \frac{\left(m_{1}+m_{2}\right)^{2}}{m_{1}m_{2}\left(m_{1}+m_{2}\right)}=\frac{\left(m_{1}m_{2}\right)n^{2}h^{2}}{8\pi^{2}r^{2}m_{1}m_{2}}$