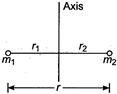
Q. A diatomic molecule is formed by two atoms which may be treated as mass points $ m_{1}$ and $ m_{2}, $ joined by a massless rod of length $r$. Then the moment of inertia of the molecule about an axis passing through the center of mass and perpendicular to rod is
J & K CETJ & K CET 2003
Solution:
Total moment of inertia will be equal to the sum of moment of inertia due to individual masses.
$I=\sum_{l=1}^{n} I_{i}$
where $I_{1}=m_{1} r_{1}{ }^{2}, \,\,\,\, I_{2} m_{2} r_{2}{ }^{2} .$
Given, $r=r_{1}+r_{2} m_{1} r_{1}=m_{2} r_{2}$
$\therefore m_{1} r_{1}=m_{2}\left(r-r_{1}\right)$
$\Rightarrow m_{1} r_{1}+m_{2} r_{1}=m_{2} r$
$\Rightarrow r_{1}\left(m_{1}+m_{2}\right)=m_{2} r$
$\Rightarrow r_{1}=\frac{m_{2} r}{\left(m_{1}+m_{2}\right)}$
Also, $r_{2}=r-r_{1} r_{2}=r-\frac{m_{2} r}{\left(m_{1}+m_{2}\right)}=\frac{m_{1} r}{m_{1}+m_{2}}$
$\therefore I=I_{1}+I_{2}=m_{1} r_{1}{ }^{2}+m_{2} r_{2}{ }^{2}$
$I=m_{1} \frac{m_{2}^{2} r^{2}}{\left(m_{1}+m_{2}\right)^{2}}+m_{2} \frac{m_{1}{ }^{2} r^{2}}{\left(m_{1}+m_{2}\right)} .$
$I=\frac{m_{1} m_{2} r^{2}}{\left(m_{1}+m_{2}\right)}=\frac{m_{1} m_{2}}{\left(m_{1}+m_{2}\right)} \cdot r^{2}$