Q.
A cylindrical tube, with its base as shown in the figure, is filled with water. It is moving down with a constant acceleration $a$ along a fixed inclined plane with angle $\theta=45^{\circ} . P_{1}$ and $P_{2}$ are pressures at points $1$ and $2$, respectively located at the base of the tube. Let $\beta=\left(P_{1}-P_{2}\right) /(\rho g d)$, where $\rho$ is density of water, $d$ is the inner diameter of the tube and $g$ is the acceleration due to gravity. Which of the following statement(s) is(are) correct?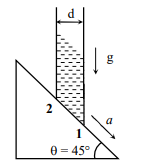
JEE AdvancedJEE Advanced 2021
Solution: