Question

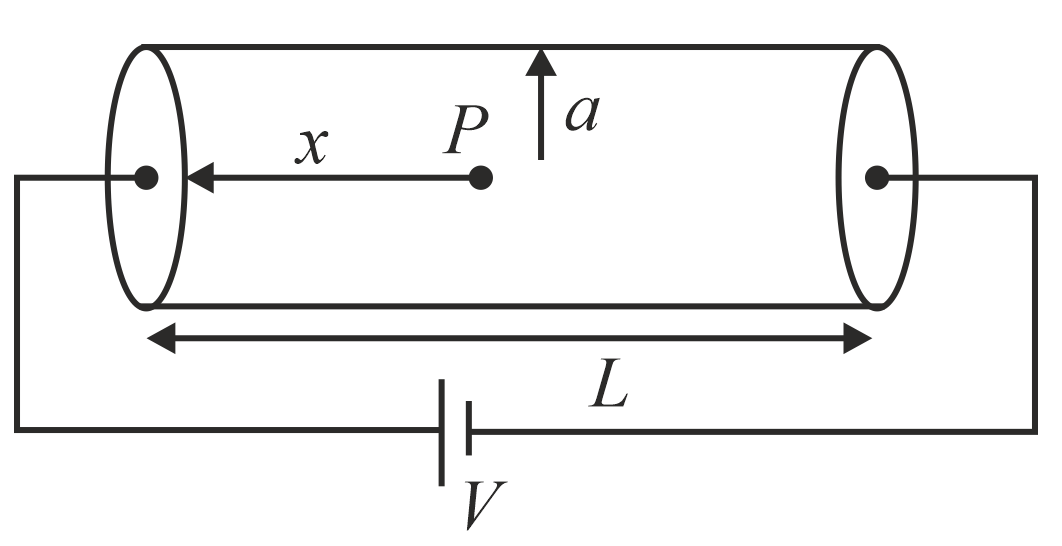
A cylindrical solid rod of length $L$ and radius $a$ is connected across a source of emf $V$ and negligible internal resistance as shown in the figure. The resistivity of the rod at point $P$ at a distance $x$ from the left end is given by $\rho =bx$ (where $b$ is a positive constant). The electric field at point $P$ is $\left(\frac{n V}{L^{2}}\right)x$ . The value of $n$ is

Answer 1

Resistance, $R=\int \frac{\rho d x}{A}=\frac{\int\limits _{0}^{L} b x d x}{A}=\frac{b L^{2}}{2 A}$
Current, $I=\frac{V}{R}=\frac{2 V A}{b L^{2}}$
Current density, $j=\frac{I}{ A}=\frac{2 V}{ b L^{2}}$
$\Rightarrow j=\sigma E$
Electric field, $E=\rho j=\frac{\left(b x\right) 2 V}{b l^{2}}=\frac{2 V}{L^{2}}x$