Q. A cylindrical plastic bottle of negligible mass is filled with $310\, ml$ of water and left floating in a pond with still water. If pressed downward slightly and released, it starts performing simple harmonic motion at angular frequency $\omega$. If the radius of the bottle is $2.5\, cm$ then $\omega$ close to : (density of water = $10^3 \; kg / m^3$)
Solution:
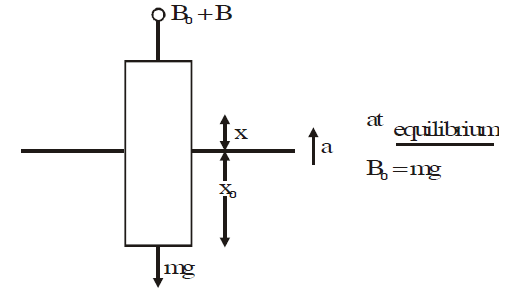
Extra Boyant force = $\delta $ Axg
$B_0 + B \times \; mg = ma$
$B= ma $
$ a =\left(\frac{\delta Ag}{m}\right)^{x} $
$ w^{2} =\frac{\delta Ag}{m} $
$w = \sqrt{\frac{10^{3} \times\pi\left(2.5\right)^{2} \times10^{-4} \times10}{310 \times10^{-6} \times10^{3}}} $
$ = \sqrt{63.30} = 7.95$