Q.
A cylindrical piston of mass $M$ slides smoothly inside a long cylinder closed at one end,
enclosing a certain mass of gas.
The cylinder is kept with its axis
horizontal. If the piston is
disturbed from its equilibrium
position, it oscillates simple harmonically. The period of oscillation will be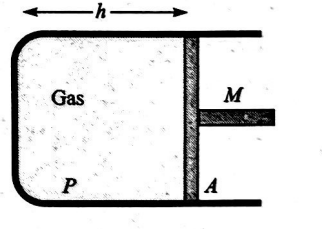
Oscillations
Solution:
