Question

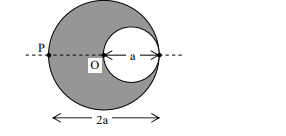
A cylindrical cavity of diameter a exists inside a cylinder of diameter $2a$ as shown in the figure. Both the cylinder and the cavity are infinity long. A uniform current density J flows along the length. If the magnitude of the magnetic field at the point $P$ is given by $\frac{ N }{12} \mu_{0} aJ $, then the value of $N$ is

Answer 1

$B =\frac{\mu_{0}\left( J \pi a ^{2}\right)}{2 \pi a }-\frac{\mu_{0}\left( J \pi a ^{2} / 4\right)}{2 \pi\left(\frac{3 a }{2}\right)}$
$B =\frac{5 \mu_{0} Ja }{12}=\frac{\mu_{0} NJa }{12}$
So $N =5$