Question

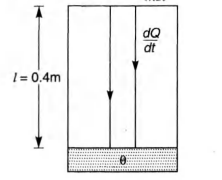
A cylindrical block of length 0.4 m and area of cross-section
0.04 m$^2$ is placed coaxially on a thin metal disc of mass 0.4
kg and of the same cross-section. The upper face of the
cylinder is maintained at a constant temperature of 400 K and
the initial temperature of the disc is 300 K. If the thermal
conductivity of the material of the cylinder is 10 W/mK and
the specific heat capacity of the material of the disc is 600
J/kg-K, how long will it take for the temperature of the disc to
increase to 350 K? Assume, for purposes of calculation, the
thermal conductivity of the disc to be very high and the
system to be thermally insulated except for the upper face of
the cylinder.

Answer 1

Let at any time temperature of the disc be $\theta$
At this moment rate of heat flow,
$ \, \, \, \, \, \frac{dQ}{dt} =\frac{KA (Delta \theta)}{l} =\frac{KA}{l} (\theta_0 -\theta)$ ...(i)
This heat is utilised in increasing the temperature of the disc.
Hence
$ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \frac{dQ}{dt} =ms \frac{d\theta}{dt} \, \, \, \, \, \, \, \, \, \, \, \, \, \, $ ...(ii)
Equating Eqs. (i) and (ii), we have
$ \, \, \, \, \, \, \, \, \, \, \, \, ms \frac{d\theta}{dt} =\frac{KA}{l}(\theta_0 -\theta)$
Therefore $ \, \, \, \, \, \frac{d\theta}{\theta_0 -\theta} =\frac{KA}{ms l}dt$
or $ \, \, \, \, \, \, \int _{300 k}^{350 k} \frac{d\theta}{\theta_0 -\theta} =\frac{KA}{ms l} \int_0^t dt$
or $[-ln (\theta_0 -\theta)]_{300 K}^{350 K} =\frac{KA}{msl}t$
$\therefore \, \, \, \, \, \, \, \, \, t=\frac{ms l}{KA}ln \bigg(\frac{\theta_0 -300}{\theta_0 - 350}\bigg)$
Substituting the values, we have
$ \, \, \, \, \, \, \, \, t=\frac{(0.4)(600)(0.4)}{(10)(0.04)}ln \bigg(\frac{400-300}{400-350}\bigg)$
$ \, \, \, \, \, \, \, \, \, \, \, t=166.32 s $