Question

A cyclist starts from the centre $O$ of a circular park of radius $1\,km$, reaches the edge $P$ of the park, then cycles along the circumference and returns to the centre- along $QO$ as shown in the figure.

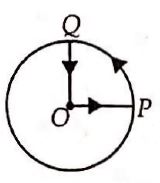
If the round trip takes ten minutes, the net displacement and average speed of the cyclist (in metre and kilometre per hour) is

• A. $0$, $1$
• B. $\frac{\pi+4}{2}$, $0$
• C. $21$, $4$, $\frac{\pi+4}{2}$
• D. $0$, $21$. $4$

Answer 1

Answer: (D)

Since the initial position coincides with the final position. So, net displacement of the cyclist = zero
Average speed of the cyclist $=\frac{\text{Total distance travelled}}{\text{Total time taken}}$
$=\frac{OP+PQ+QO}{10}km \,min^{-1}$
$=\frac{1+\frac{\pi}{2}\times1+1}{10}km \,min^{-1}$
$=\frac{\pi+4}{20}km\,min^{-1}$
$=\frac{\pi+4}{20}\times60km \,h^{-1}$
$=21.4\,km \,h^{-1}$