Question

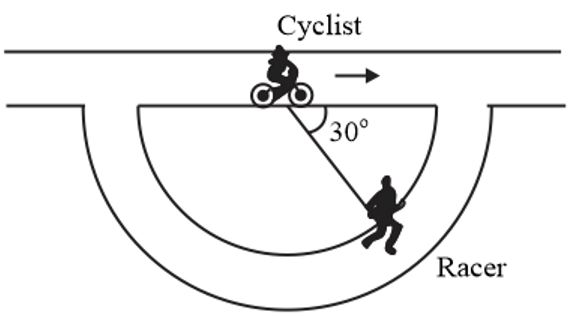
A cyclist is moving with a constant acceleration of $1.2 \, m \, s^{- 2}$ on a straight track. A racer is moving on a circular path of the radius $150 \, m \, $ at a constant speed of $15 \, m \, s^{- 1}$ . Find the magnitude of the velocity of racer which is measured by the cyclist has reached a speed of $20 \, m \, s^{- 1}$ for the position represented in the figure.

• A. $18.03 \, m \, s^{- 1}$
• B. $25ms^{- 1}$
• C. $20 \, m \, s^{- 1}$
• D. $15 \, m \, s^{- 1}$

Answer 1

Answer: (A)

Let $\overset{ \rightarrow }{v}_{c}$ = actual velocity of cyclist along $x-axis$
$\overset{ \rightarrow }{v}_{r}$ = the velocity of racer along tangent of circular path (shown in figure)
$\therefore \, $ $\overset{ \rightarrow }{v}_{r c}= \, \overset{ \rightarrow }{v}_{r}- \, \overset{ \rightarrow }{v}_{c}$


Hence $\overset{ \rightarrow }{v}_{c}=20 \, \hat{i}$
$\overset{ \rightarrow }{v}_{r c}=V_{r}cos 30^{o}\hat{j}+V_{r}sin ⁡ 30^{o}\hat{i}$
Or $\overset{ \rightarrow }{v}_{r}=15cos 30\hat{j}+15sin ⁡ 30\hat{i}$
$=\frac{15 \sqrt{2}}{2} \, \hat{j}+\frac{15}{2} \, \hat{i}$
$\therefore $ $\overset{ \rightarrow }{v}_{r c}= \, \overset{ \rightarrow }{v}_{r}- \, \overset{ \rightarrow }{v}_{c}$
$=\frac{15 \sqrt{3}}{2} \, \hat{j}+\frac{15 \sqrt{3}}{2} \, \hat{j}$
$= \, -12.5 \, \hat{i}+\frac{15 \, \sqrt{3}}{2} \, \hat{j}$
$\therefore\left|\vec{v}_{r c}\right|=\sqrt{(-12.5)^2+\left(\frac{15 \sqrt{3}}{2}\right)^2}$
$=18.03 \, ms^{- 1}$