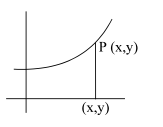
Question

A curve is such that the area of the region bounded by the co-ordinate axes, the curve & the ordinate of any point on it is equal to the cube of that ordinate. The curve represents

• A. a pair of straight lines
• B. a circle
• C. a parabola
• D. an ellipse

Answer 1

Answer: (C)

$\int\limits_0^x f(x) d x=y^3$

Differentiating
$f(x)=3 y^2 \cdot \frac{d y}{d x} $
$y=3 y^2 \frac{d y}{d x} \quad \Rightarrow \quad y=0 \text { (rejected) }$
$\text { or } 3 ydy = dx $
$\frac{3 y^2}{2}=x+c \Rightarrow \text { parabola } \Rightarrow C$