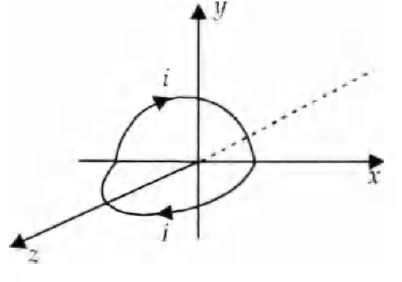
Question

A current loop consists of two identical semicircular parts each of radius $R$, one lying in the $x-y$ plane and the other in $x-z$ plane. If the current in the loop is $i$. The resultant magnetic field due to the two semicircular parts at their common centre is

• A. $\frac{\mu_0 i}{2\sqrt2 R}$
• B. $\frac{\mu_0 i}{2R}$
• C. $\frac{\mu_0 i}{4R}$
• D. $\frac{\mu_0 i}{\sqrt2 R}$

Answer 1

Answer: (A)

The loop mentioned in the question must look
like one as shown in the figure.

Magnetic field at the centre due to semicircular loop lying in $x-y$ plane,
$B_{x y}=\frac{1}{2}\left(\frac{\mu_{0} i}{2 R}\right)$ negative $z$ direction.
Similarly field due to loop in $x$-z plane, $B_{x z}=\frac{1}{2}\left(\frac{\mu_{0} i}{2 R}\right)$ in negative y direction.
$\therefore$ Magnitude of resultant magnetic field,
$B =\sqrt{B_{x y}^{2}+B_{x z}^{2}}=\sqrt{\left(\frac{\mu_{0} i}{4 R}\right)^{2}+\left(\frac{\mu_{0} i}{4 R}\right)^{2}}$
$=\frac{\mu_{0} i}{4 R} \sqrt{2}=\frac{\mu_{0} i}{2 \sqrt{2} R}$