Question

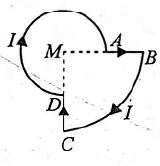
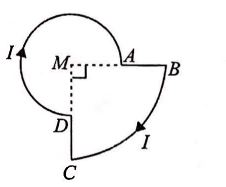
A current $I$ is flowing through a loop. The direction of the current and the shape of the loop are as shown in the figure The magnetic field at the centre of the loop is $\frac{\mu_{0} I}{R}$ times (Here, $MA=R, MB=2R, \angle DMA= 90^{\circ})$

• A. $\frac{5}{16}$, out of the plane of the paper
• B. $\frac{5}{16}$, into the plane of the paper
• C. $\frac{7}{16}$, out of the plane of the paper
• D. $\frac{7}{16}$, into the plane of the paper

Answer 1

Answer: (D)

Magnetic field at the centre $M$ due to current through the curved portion $DA$ is
$B_{1}=\frac{\mu_{0}I}{4\pi R} \times\left(\frac{3\pi}{2}\right)$
into the plane of the paper
$=\frac{3\mu_{0}I}{8R}$ into the plane of the paper
Magnetic field at the centre $M$ due to current through the straight portion $AB$ is $B_{2}=0$
($\because$ point $M$ lies on the axis of the straight portion $AB$ )
Magnetic field at the centre $M$ due to current through the curved portion $BC$ is
$B_{3}=\frac{\mu_{0}I}{4\pi\left(2R\right)}\times\frac{\pi}{2}$ into the plane of the paper
$=\frac{\mu_{0}I}{16R}$ into the plane of the paper
Magnetic field at the centre $M$ due to current through the straight portion $CD$ is $B_{4}=0 $
($\because$ point $M$ lies on the axis of the straight portion $CD$ )
The resultant magnetic field at $M$ is
$B=B_{1}+B_{2}+B_{3}+B_{4}$
$=\frac{3\mu_{0}I}{8R}+0+\frac{\mu_{0}I}{16R}+0$
$=\frac{3\mu_{0}I}{8R}+\frac{\mu_{0}I}{16R}$
$=\frac{7\mu_{0}I}{16R}$ into the plane of the paper