Question

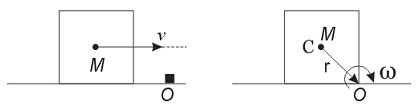
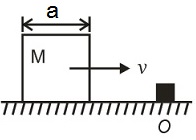
A cubical block of side moving with a velocity $v$ on a horizontal smooth plane as shown. It hits a ridge at point $O$ and sticks to it (collision is perfectly inelastic). The angular speed of the block after it hits $O$ is

• A. $\frac{3 v}{4 a}$
• B. $\frac{3 v}{2 a}$
• C. $\frac{\sqrt{3} \textit{v}}{\sqrt{2} \textit{a}}$
• D. Zero

Answer 1

Answer: (A)

Net torque about $O$ is zero.
Therefore, angular momentum $\left(L\right)$ about point $O$ will be conserved
or, $\textit{L}_{\text{i}}=\textit{L}_{\text{f}}$
$\operatorname{Mv}\left(\frac{a}{2}\right)=I_{0} \omega=\left(I_{\text {com }}+ Mr ^{2}\right) \omega$
$=\left\{\left(\frac{ Ma ^{2}}{6}\right)+M\left(\frac{a^{2}}{2}\right)\right\} \omega=\frac{2}{3} Ma ^{2} \omega$
$\therefore \quad \omega=3 v / 4 a$