Q.
A cube of side $L$ has point charges $+q$ located at its seven vertices and $-q$ at remaining one vertex. The electric field at its center is found to be
$|\vec{ E }|=\alpha\left(\frac{q}{4 \pi \in_{0} L ^{2}}\right)$.The magnitude $=f$ constant $\alpha$ is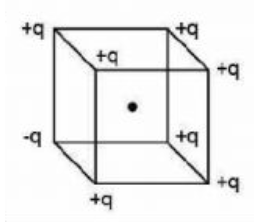
TS EAMCET 2020
Solution:

