Question

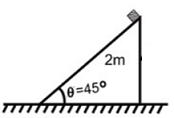
A cube of mass $m$ is placed on top of a wedge of mass $2 \, m$ , as shown in figure. There is no friction between the cube and the wedge. The minimum co-efficient of friction between the wedge and the horizontal surface, so that the wedge does not move is

• A. $0.1$
• B. $0.2$
• C. $0.3$
• D. $\frac{1}{\sqrt{2}}$

Answer 1

Answer: (B)

The normal reaction between the wedge and the block is
$N^{'}=mgcos\theta $
So the net horizontal force on the wedge is
$F=mgcos \theta sin ⁡ \theta $
The normal reaction between the wedge and the ground is
$N=2 \, mg+mgcos^{2} \theta $
$N=2 \, mg+mg \, cos^{2}\theta $
Now, $F=\mu N$ gives
$\mu =\frac{F}{N}=\frac{m g cos \theta sin ⁡ \theta }{2 \, m g + m g cos^{2} ⁡ \theta }$
$=\frac{cos \theta sin ⁡ \theta }{2 + cos^{2} ⁡ \theta }$
For $\theta =45^{o}, \, \, \mu =0.2$