Question

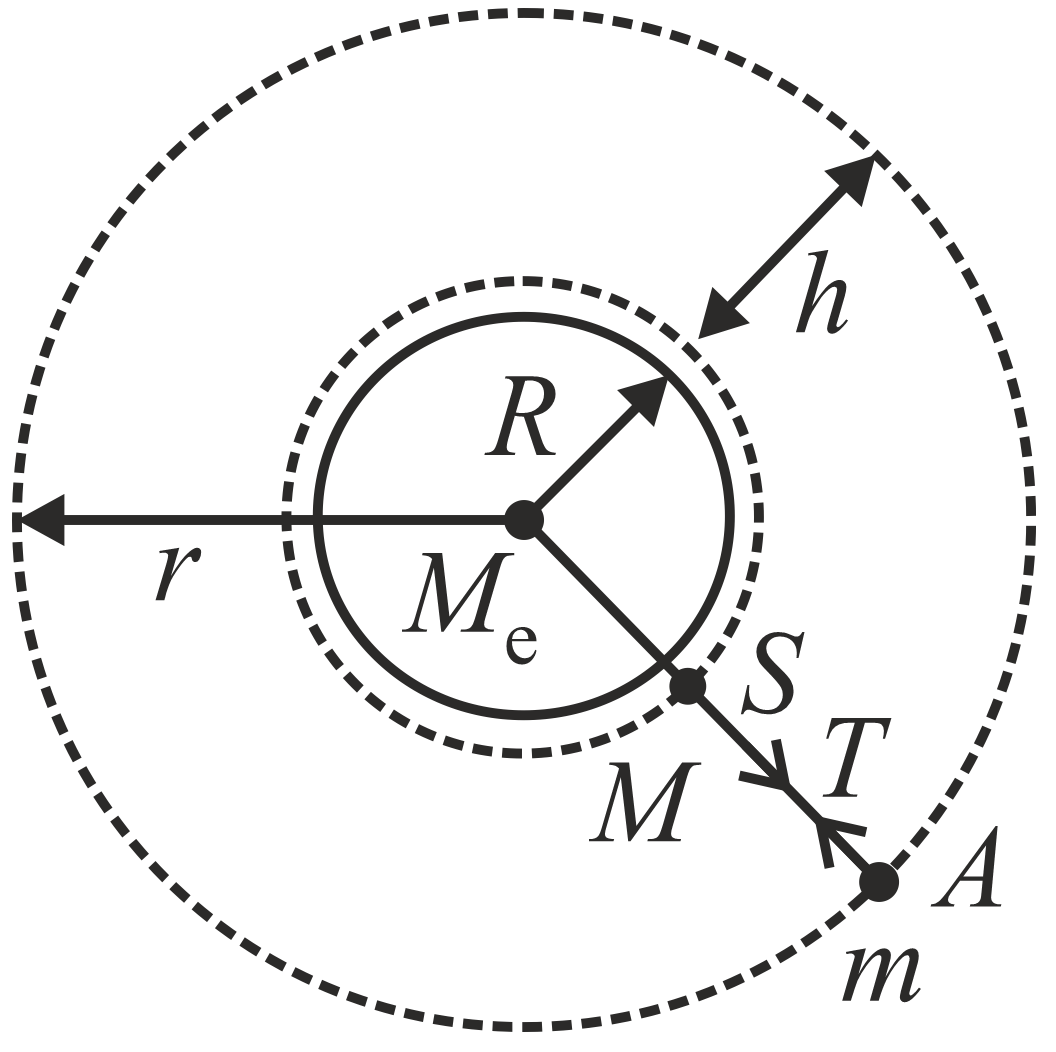
A cord of length $h=64\,m$ is used to connect an astronaut ( $m=100\,kg$ ) to a spaceship ( $M\gg m$ ) which is orbiting near the earth's surface as shown in the figure. Assuming that the spaceship and the astronaut fall on a straight line from the earth's centre, then the tension in the cord is close to [ $R=6400\,km$ ]

• A. $3\times 10^{- 2}N$
• B. $2\times 10^{- 2}N$
• C. $4\times 10^{- 2}N$
• D. $5\times 10^{- 2}N$

Answer 1

Answer: (A)

According to given problem, the mass of satellite $M$ is much greater than that of astronaut $m$ . So the centre of mass of the system will be close to satellite and as the satellite is orbiting close to the surface of earth, the equation of motion of the system $\left(S+A\right)$ will be-
$\frac{\left(GM\right)_{e } \left(M ⁡ + m ⁡\right)}{R ⁡^{2}}=\left(M ⁡ + m ⁡\right)R⁡\left(\omega \right)^{2}$
i.e., $R \left(\omega \right)^{2}=\frac{\left(GM\right)_{e ⁡}}{R ⁡^{2}}=g\ldots $(i)
And the equation of motion of the astronaut will be
$\frac{GM_{e } m ⁡}{r ⁡^{2}}+T⁡=m⁡r⁡\omega ^{2}$, i.e., $T⁡=m⁡\left[r ⁡ \omega ^{2} - \frac{\text{GM}_{e ⁡}}{r ⁡^{2}}\right]$
In the light of equation (i), above equation reduces to
$T =mg\left[\frac{r ⁡}{R ⁡} - \left(\frac{R ⁡}{r ⁡}\right)^{2}\right]=\text{mg}\left[\frac{\left(R ⁡ + h ⁡\right)}{R ⁡} - \frac{R ⁡^{2}}{\left(R ⁡ + h ⁡\right)^{2}}\right]$
$\left[\text{as} \,r = R ⁡ + h ⁡\right]$
or $T =mg\left[\left(1 + \frac{h ⁡}{R ⁡}\right) - \left(1 + \frac{h ⁡}{R ⁡}\right)^{- 2}\right]=\frac{3 \text{mgh}}{R ⁡}$
$\left[\text{as}\, \left(1 + \frac{h }{R ⁡}\right)^{- 2} \sim eq 1 - \frac{2 h ⁡}{R ⁡}\right]$
So substituting the given data,
$T =\frac{3 \times 100 \times 10 \times 64}{6400 \times 10^{3}}=3\times 10^{- 2}N$