Q.
A cord is wrapped on a pulley (disk) of mass $M$ and radius $R$ as shown in figure. To one end of the cord, a block of mass $M$ is connected as shown and to other end in (a) a force of $2 \, M g$ and in (b) a block of mass $2 \, M$ . Let angular acceleration of the disk in $A$ and $B$ is $\alpha _{A}$ and $\alpha _{B}$ respectively, then (cord is not slipping on the pulley)
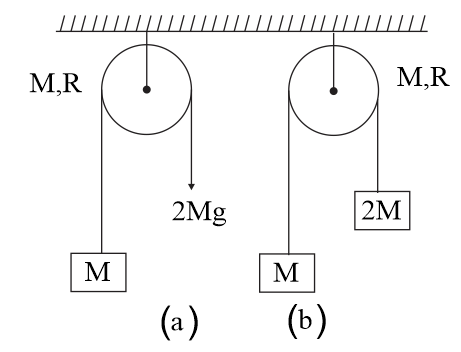
NTA AbhyasNTA Abhyas 2022
Solution:
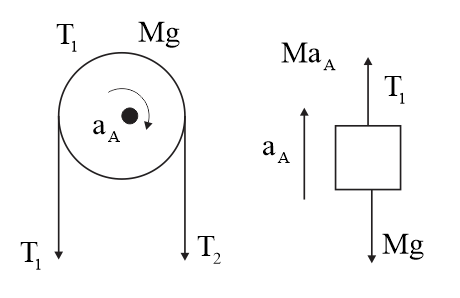
In figure, $\left(T_{2} - T_{1}\right)R=\frac{M R^{2}}{2}\left(\alpha \right)_{A}$
$T_{1}-Mg=Ma_{A}$
$T_{2}=2Mg$ $$
$a_{A}=R\alpha _{A}$
$R\left(\right. 2 M g - M g - M a_{A} \left.\right)=\frac{M R^{2}}{2}\left(\alpha \right)_{A}$
$g-R\alpha _{A}=\frac{R \alpha _{A}}{2}$
$\alpha _{A}=\frac{2 g}{3 R}$
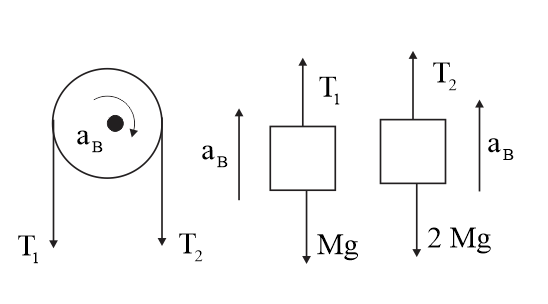
From Figure, $\left(T_{2} - T_{1}\right)\times R=\frac{M R^{2}}{2}\left(\alpha \right)_{B}$
$T_{1}-Mg=Ma_{B}$
$2Mg-T_{2}=2Ma_{B}$
$a_{B}=R\alpha _{B}$
$\Rightarrow $ $\alpha _{B}=\frac{2 g}{7 R}$
So, $\alpha _{A}>\alpha _{B}$

In figure, $\left(T_{2} - T_{1}\right)R=\frac{M R^{2}}{2}\left(\alpha \right)_{A}$
$T_{1}-Mg=Ma_{A}$
$T_{2}=2Mg$ $$
$a_{A}=R\alpha _{A}$
$R\left(\right. 2 M g - M g - M a_{A} \left.\right)=\frac{M R^{2}}{2}\left(\alpha \right)_{A}$
$g-R\alpha _{A}=\frac{R \alpha _{A}}{2}$
$\alpha _{A}=\frac{2 g}{3 R}$

From Figure, $\left(T_{2} - T_{1}\right)\times R=\frac{M R^{2}}{2}\left(\alpha \right)_{B}$
$T_{1}-Mg=Ma_{B}$
$2Mg-T_{2}=2Ma_{B}$
$a_{B}=R\alpha _{B}$
$\Rightarrow $ $\alpha _{B}=\frac{2 g}{7 R}$
So, $\alpha _{A}>\alpha _{B}$