Q.
A convex lens of focal length 15 cm and a concave mirror of
focal length 30 cm are kept with their optic axis PQ and RS
parallel but separated in vertical direction by 0.6 cm as
shown.
The distance between the lens and mirror is 30 cm. An
upright object AB of height 1.2 cm is placed on the optic axis
PQ of the lens at a distance of 20 cm from the lens. If A' B' is
the image after refraction from the lens and the reflection
from the mirror, find the distance of A'B' from the pole of
the mirror and obtain its magnification. Also locate positions
of A' and B' with respect to the optic axis RS.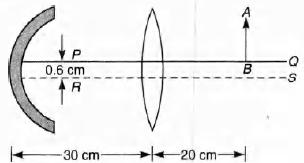
IIT JEEIIT JEE 2000
Solution:
(a) Rays coming from object AB first refract from the lens
and then reflect from the mirror.
Refraction from the lens
$ \, \, \, \, \, \, \, \, \, u=$ - 20 cm, f = +15 cm
Using lens formula $\frac{1}{v}-\frac{1}{u}=\frac{1}{f} \, \, \, \Rightarrow \, \, \frac{1}{v}-\frac{1}{-20}=\frac{1}{15}$
$\therefore $ v = + 60 cm
and linear magnification,$m_1=\frac{v}{u}=\frac{+60}{-20}=-3$
i.e. first image formed by the lens will be at 60 cm from it
(or 30 cm from mirror) towards left and 3 times
magnified but inverted. Length of first image $A_1 B_1$
would be 1.2 x 3 = 3.6 cm (inverted).
Reflection from mirror Image formed by lens $(A_1 B_1)$
will behave like a virtual object for mirror at a distance of
30 cm from it as shown. Therefore u = +30 cm,
f = - 30 cm.
Using mirror formula, $\frac{1}{v}+\frac{1}{u}=\frac{1}{f} \, \, \, or \, \, \, \frac{1}{v}+\frac{1}{30}=-\frac{1}{30}$
$\therefore $ v = - 15 cm
and linear magnification,
$ \, \, \, \, \, \, \, \, \, m_2=-\frac{v}{u}=-\frac{-15}{+30}=+\frac{1}{2}$
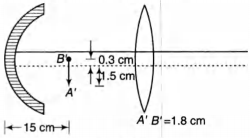
i.e. final image A'B' will be located at a distance of 15 cm
from the mirror (towards right) and since magnification is
$+\frac{1}{2}$, length of final image would be 3.6 x $\frac{1}{2}$ =1.8 cm
$\therefore $ A' B' = 1.8 cm
Point $B_1$ is 0.6 cm above the optic axis of mirror,
therefore, its image B' would be (0.6)$\big(\frac{1}{2}\big)$ = 0.3 cm
above optic axis. Similarly, point $A_1$ is 3 cm below the
optic axis, therefore, its image A' will be 3 x $\frac{1}{2}$ = 1.5 cm
below the optic axis as shown below
Total magnification of the image,
$ \, \, \, \, \, \, \, m=m_1 \times m_2 =(-3)\big(+\frac{1}{2}\big)=-\frac{3}{2}$
$\therefore \, \, $ A ' B ' = (m )(AB) =$\big(-\frac{3}{2}\big)(1.2)=$ -1.8 cm
Note that, there is no need of drawing the ray diagram if
not asked in the question
NOTE With reference to the pole of an optical instrument (whether it
is a lens or a mirror) the coordinates of the object ($X_o, Y_o$) are
generally known to us. The corresponding coordinates of image
($X_i, Y_i$) are found as follows
$ \, \, \, \, \, \, \, \, \, \, \, X_i$ is obtained using $\frac{1}{v} \pm \frac{1}{u}=\frac{1}{f}$
Here, vis actually $X_i$ and u is $X_p$ ie, the above formula can be written
as $\frac{1}{X_i} \pm \frac{1}{X_o}=\frac{1}{f}$
Similarly, $Y_i$ is obtained from m=$\frac{l}{o}$
Here, l is $Y_i$ and 0 is $Y_o$ i.e., the above formula can be written as
$m=Y_i/Y_o \, \, or \, \, Y_i=m Y_o.$