Question

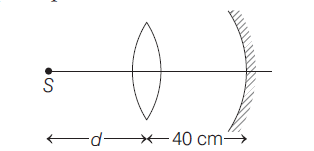
A converging mirror is placed on the right hand side of a converging lens as shown in the figure. The focal length of the mirror and the lens are $20 \,cm$ and $15 \,cm$, respectively. The separation between the lens and the mirror is $40 \,cm$ and their principal axis coincide. A point source is placed on the principal axis at a distance $d$ to the left of the lens. If the final beam comes out parallel to the principal axis, then the value of $d$ is

• A. 4 cm
• B. 8 cm
• C. 12 cm
• D. 16 cm

Answer 1

Answer: (C)

Image of lens will act as object for mirror.
Here, $v_{1}+u_{2}=40 \,cm$
Lens formula, $\frac{1}{f_{1}}=\frac{1}{u_{1}}-\frac{1}{v_{1}}$
Mirror formula, $\frac{1}{f_{2}}=\frac{1}{u_{2}}+\frac{1}{v_{2}}$
For final image, $v_{2}=\infty$
So, $\frac{1}{f_{2}}=\frac{1}{u_{2}}$
$\Rightarrow u_{2}=15\, cm$
Now, $v_{1}=40-15=25 \,cm$
So, value of $u_{1}$ should be
$\frac{1}{20}=\frac{1}{u_{1}}-\frac{1}{25} \Rightarrow \frac{1}{u_{1}}=\frac{1}{20}+\frac{1}{25}$
$u_{1}=100 / 9 \,cm \Rightarrow u_{1}=11.11 \,cm$
$=12 \,cm$