Question

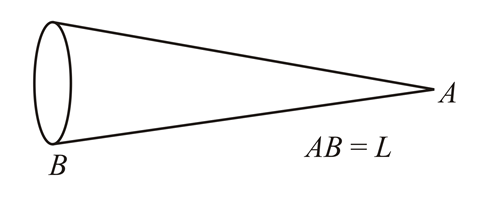
A cone made of insulating material has a total charge $Q$ spread uniformly over its sloping surface having a slant length $L$ . The energy required to take a test charge $q$ from infinity to apex $A$ of the cone will be

• A. $\frac{ Qq }{2 \pi \varepsilon_{0} L}$
• B. $\frac{ Qq }{4 \pi \varepsilon_{0} L}$
• C. $-\frac{ Qq }{3 \pi \varepsilon_{0} L }$
• D. $\frac{ Qq }{8 \pi \varepsilon_{0} L}$

Answer 1

Answer: (A)

$\sigma =\frac{Q}{\pi RL}$
$L$ = Slant height
$dQ=\sigma \times \left(2 \pi r\right)dx$
= Charge on the elementary ring
$dQ=\frac{Q}{\pi RL}\times 2\pi rdx=\frac{Q}{LR}\left(2 rdx\right)$ ... (1)
By similarity of triangles :
$\frac{R}{L}=\frac{r}{x} \, \Rightarrow r=\frac{R}{L}x$ ... (2)
By (1) and (2) we get
$dQ=\frac{Q}{LR}\times 2\frac{R}{L}xdx=\frac{2 Q}{L^{2}}xdx$
$\therefore $ the electric potential at A due to ring is
$dV=\frac{kdQ}{x}=\frac{k}{x}\frac{\left(2 Q\right)}{L^{2}}xdx$
$\therefore $ Total potential at A is
$V=\displaystyle \int dv=\frac{2 kQ}{L^{2}}\displaystyle \int _{0}^{L}dx=\frac{2 kQ}{L^{2}}\times L$
$V=\frac{2 kQ}{L}$
$\therefore $ Work done to shift a charge q from infinity to point $A$ is = $qV$
$W=\frac{2 kqQ}{L} \, =2\times \frac{1}{4 \pi ϵ_{0}}\frac{qQ}{L}=\frac{qQ}{2 \pi ϵ_{0} L}$