Q.
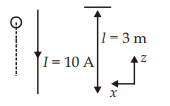
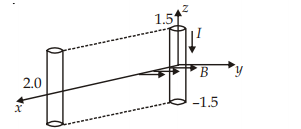
A conductor lies along the $z$ -axis at $-1.5 \leq z<1.5 \,m$ and carries a fixed current of $10.0 A$ in $-\hat{a}_{z}$ direction (see figure). For a field $\vec{B}=3.0 \times 10^{-4} e^{-0.2 x} \hat{a}_{y} T$, find the power required to move the conductor at constant speed to $x=2.0 m , y=0 \,m$ in $5 \times 10^{-3} \,s$. Assume parallel motion along the $x$ -axis
Solution: