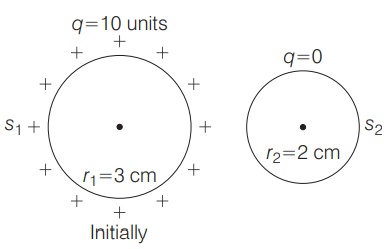
Question

A conducting sphere $S_{1}$ of radius $r_{1}$ is connected by a conducting wire to another conducting sphere $S_{2}$ of radius $r_{2}$, where $r_{1}=3\, cm$ and $r_{2}=2\,cm$. Before they are connected, $S_{1}$ carries charge of $10$ units. The electric potential at the point which is at a distance $4\, cm$ from the centre of $S_{1}$ and a distance $3\, cm$ from the centre of $S_{2}$ is

• A. $\frac{1}{4 \pi \varepsilon_{0}} \frac{17}{6}$
• B. $\frac{1}{4 \pi \varepsilon_{0}} \frac{3}{2}$
• C. $\frac{1}{4 \pi \varepsilon_{0}} \frac{1}{6}$
• D. $\frac{1}{4 \pi \varepsilon_{0}} \frac{17}{12}$

Answer 1

Answer: (A)

When spheres are connected, charges are redistributed such that potential on their surfaces
are same.

So, we have
$q_{1}+q_{2}=10$
and $\frac{k q_{1}}{r_{1}}=\frac{k q_{2}}{r_{2}}$
$\Rightarrow \frac{q_{1}}{3}=\frac{q_{2}}{2}$
Hence, $q_{1}=6$ units and $q_{2}=4$ units.
Now, potential at some point $P$ distant $4\, cm$ from $s_{1}$ and $3\, cm$ from $s_{2}$ is
$V =\frac{k q_{1}}{r_{1}}+\frac{k q_{2}}{r_{2}}=k \frac{6}{4}+ k \frac{4}{3}$
$=k\left(\frac{3}{2}+\frac{4}{3}\right)=k \frac{17}{6} V$
$=\frac{1}{4 \pi \varepsilon_{0}} \frac{17}{6} V$