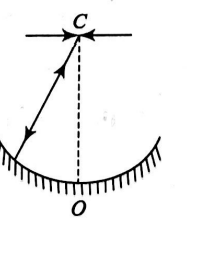
Q. A concave mirror is placed on a horizontal table with its axis directed vertically upward. Let $O$ be the pole of the mirror $C$ its center of curvature and $F$ is the focus. A point object is placed at $C$. It has a real image, also located at $C$. If the mirror is now filled with water, the image will be
Ray Optics and Optical Instruments
Solution:
When there is no water in the mirror, the rays of light are incident normally on the mirror and retrace their path. So, we get an image coincident with the object as shown in the figure. When the mirror is filled with water, then the equivalent focal length $F$ is given by
$\frac{1}{F}=\frac{1}{f_{\text {water lens }}}+\frac{1}{f_{\text {concave mirror }}}+\frac{1}{f_{\text {water lens }}}$
or $\frac{1}{F}=2 \times \frac{1}{f_{\text {water lens }}}+\frac{1}{f_{\text {concave mirror }}}$
or $\frac{1}{F}=2(\mu-1)\left(\frac{1}{R}\right)+\frac{1}{R}$
or $\frac{1}{F}=\frac{2(\mu-1)}{R}+\frac{2}{R}$
or $\frac{1}{F}=\frac{2 \mu}{R}$ or $F=\frac{R}{2 \mu}$
Clearly, focal length of the new optical system in less than the original. So, the object is effectively at a distance greater than twice the focal length. So, the real image will be formed between $F$ and $C$.