1. Tardigrade
  2. Question
  3. Physics
  4. A concave mirror has radius of curvature of 40 cm. It is at the bottom of a glass that has water filled up to 5 cm (see figure). If a small particle is floating on the surface of water, its image as seen, from directly above the glass, is at a distance d from the surface of water. The value of d is close to: (Refractive index of water = 1.33)

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

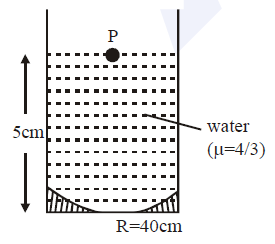
Q. A concave mirror has radius of curvature of $40\, cm$. It is at the bottom of a glass that has water filled up to $5\, cm$ (see figure). If a small particle is floating on the surface of water, its image as seen, from directly above the glass, is at a distance d from the surface of water. The value of d is close to : (Refractive index of water $= 1.33$)Physics Question Image

JEE MainJEE Main 2019Ray Optics and Optical Instruments

Solution:

Light incident from particle P will be reflected at mirror $u = -5cm , f=- \frac{R}{2} = - 20 cm $
$ \frac{1}{v} + \frac{1}{u} = \frac{1}{f} $
$ v_{1} = + \frac{20}{3} cm $
This image will act as object for light getting refracted at water surface
So, object distance $ d = 5+ \frac{20}{3} = \frac{35}{3} cm $ below water surface.
After refraction, final image is at
$ d' = d \left(\frac{\mu_{2}}{\mu_{1}}\right) $
$ = \left(\frac{35}{3}\right) \left(\frac{1}{4/3}\right) $
$ = \frac{35}{4} = 8.75 cm$
$ \approx8.8 cm $

Solution Image