Question

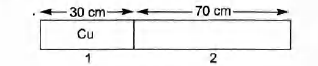
A composite rod is made by joining a copper rod , end to end
with a second .rod of different material but of the same
cross-section .At $25 ^{\circ}C,$the composite rod is 1 m in length, of
length of the composite rod increases by 1.91 mm
When the composite rod is not allowed to expand by holding
it between two rigid walls , it is found that the length of the
two constituents do not change with the rise of temperature
Find the Young's modules and the coefficient of linear
expansion of the second rod
(Given Coefficient of linear expansion of copper
$=1.7 \times 10^{-5} \, per \, \,{}^{\circ }C,$ Young's modulus of copper
=1.3 $\times 10^{11}N/m^2$

Answer 1

$\Delta l = l\alpha \Delta \theta$
$\Delta l =\Delta l_1 + \Delta l_2$
$(1.91 \times 10^{-1})=0.3 \times 1.7 \times 10^{-5} \times 100 + \alpha \times 0.7 \times 100$
Solving this equation, we get,$\alpha = 2 \times 10^{-5} \, per \,{}^{\circ C}$
Length of two rods will not change if force on joint due to
thermal stress from both sides is equal.
$i.e.,, \, \, \, \, \, \, \, \, \, \, \, \, \, F_1 =F_2$
$or \, \, \, \, \, Y_1 \times \bigg(\frac{\Delta l_1}{l_1}\bigg) \times \, A \, Y_2 \times \bigg(\frac{\Delta l_2}{l_2}\bigg) \times A$
or $Y_1 \times \alpha_1 \times \Delta \theta =Y_2 \times \alpha_2 \times \Delta\theta$
$\therefore \, \, \, \, \, \, \, \, \, \, Y_2 =\frac{\alpha_1 Y_1}{\alpha_2} =\frac{\alpha_{Cu}Y_{Cu}}{\alpha_2} $
$ \, \, \, \, \, \, \, \, =\frac{(17 \times 10^{-5})(1.3 \times 10^{11})}{(2.0 \times 10^{-5})}$
$\, \, \, \, \, \, \, \, \, \, \, \, \, \, =1105 \times 10^{11} N/m^2$