Q.
A composite block is made of slabs $A.B C,D$ and $E$ of different thermal conductivities (given in terms of a constant $K$) and sizes (given in terms of length, $L$) as shown in the figure. All slabs are of same width. Heat $Q$ flows only from left to right through the blocks. Then, in steady state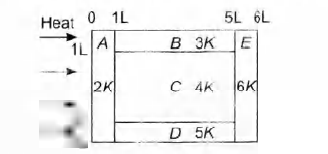
IIT JEEIIT JEE 2011Thermodynamics
Solution:
Thermal resistance R =$\frac{l}{KA}$
$\therefore R_A =\frac{L}{(2K)(4Lw)}$ (Here w = width)
$=\frac{1}{8Kw},$
$R_B =\frac{4L}{3K(Lw)}=\frac{4}{3Kw}$
$R_C =\frac{4L}{(4K)(2Lw)}=\frac{1}{2 Kw}$
$R_D =\frac{4L}{(5K)(Lw)}=\frac{4}{5 Kw}$
$R_E =\frac{L}{(6K)(Lw)}=\frac{1}{6 Kw}$
$R_A :R_B:R_C:R_D:R_E$
$=15 :160:60:96:12$
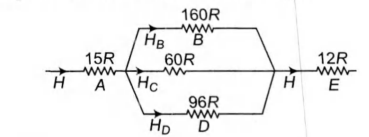
So, let us write, $R_A = 15 R, R_B = 160 R$ etc and draw a simple electrical circuit as shown in figure
$H$ = Heat current = Rate of heat flow.
$H_A=H_E=H $
$\therefore $ Option (a) is correct.
In parallel current distributes in inverse ratio of resistance.
$\therefore H_B :H_C :H_D =\frac{1}{R_B}:\frac{1}{R_C}: \frac{1}{R_D}$
$=\frac{1}{160}:\frac{1}{60}:\frac{1}{96}$
$\therefore H_B =\left(\frac{9}{9+24+15}\right)H=\frac{3}{16}H$
$ H_c =\left(\frac{24}{9+24+15}\right)H=\frac{1}{2}H$
and $H_D =\left(\frac{15}{9+24+15}\right)H=\frac{5}{16}H$
$H_C=H_B+H_D$
$\therefore $ Option (d) is correct
Temperature difference (let us call it $T$)
= (Heat current) x (Thermal resistance)
$T_A=H_A R_A=(H)(15R)=15 HR$
$T_B=H_B R_B =\left(\frac{3}{16}H\right)(160 R)=30 HR$
$T_C=H_C R_C=\left(\frac{1}{2}H\right)(60 R)=30 HR$
$T_D=H_D R_D= \left(\frac{5}{16}H\right)(96 R)=30 HR$
$T_E=H_E R_E=(H)(12R)=12 HR$
Here, $T_E$ is minimum.