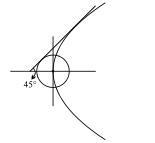
Q. A common tangent is drawn to the circle $x^2 + y^2 = c^2$ and the parabola $y^2 = 4ax$. If the angle which this tangent makes with the axis of $x$ is $\frac{\pi}{4}$ then the relationship between a and c is $(a, c > 0)$
Conic Sections
Solution:
$T$ is$ Y= mx+\frac{a}{m} \Rightarrow m^{2}x - my +a=0$
$ \therefore\left|\frac{a}{\sqrt{m^{4}+m^{2}}}\right|=c$
$a ^2 = c^2 (m^4 + m^2 ) (m = tan 45^{\circ})$
$ a^ 2 = 2c^2 \Rightarrow a = \sqrt{2} c$