Question

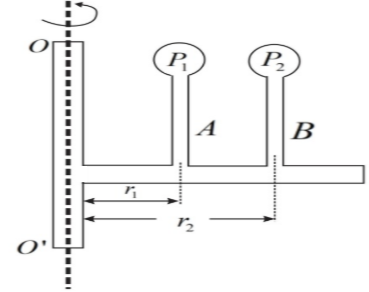
A closed tube filled with water is rotating uniformly in a horizontal plane about the axis $OO'$ as shown in the figure. The manometers $A$ and $B$ which are fixed on the tube at distances $r_{1}$ and $r_{2}$ , indicate pressures $P_{1}$ and $P_{2}$ respectively. The angular velocity ( $\omega $ ) of the tube is

• A. $\omega =\sqrt{\frac{2 \left(P_{2} - P_{1}\right)}{\rho \left(r_{2}^{2} - r_{1}^{2}\right)}}$
• B. $\omega =\sqrt{\frac{2 \left(P_{2} + P_{1}\right)}{\rho \left(r_{2}^{2} - r_{1}^{2}\right)}}$
• C. $\omega =\sqrt{\frac{2 \left(P_{2} + P_{1}\right)}{\rho \left(r_{2}^{2} + r_{1}^{2}\right)}}$
• D. $\omega =\sqrt{\frac{2 \left(P_{2} - P_{1}\right)}{\rho \left(r_{2}^{2} + r_{1}^{2}\right)}}$

Answer 1

Answer: (A)

Consider the condition of equilibrium for the mass of water contained between cross section separated by x and $x+dx$ from rotation axis.
$dp=\rho \omega ^{2}xdx$ ;
$\displaystyle \int _{p_{1}}^{p_{2}} d p=\displaystyle \int _{r_{1}}^{r_{2}} \rho \omega ^{2}xdx$


$p_{2}-p_{1}=\rho \left(\omega \right)^{2}\left[\frac{x^{2}}{2}\right]_{r_{1}}^{r_{2}}=\rho \left(\omega \right)^{2}\left(\frac{r_{2}^{2} - r_{1}^{2}}{2}\right)$
$\omega =\sqrt{\frac{2 \left(P_{2} - P_{1}\right)}{\rho \left(r_{2}^{2} - r_{1}^{2}\right)}}$