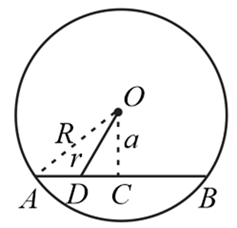
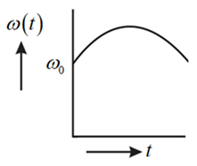
Question

A circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given an angular velocity $\omega _{0}$ . When the tortoise moves along a chord of the platform with a constant velocity (w.r.t. the platform), which of the following graphs shows properly the variation of angular velocity of the platform with the time $t$ ?

• A.
• B.
• C.
• D.

Answer 1

Answer: (C)

As there is no external torque, angular momentum will remain constant. When the tortoise moves from $A$ to $C$ , figure, moment of inertia of the platform and tortoise decreases. Therefore, angular velocity of the system increases. When the tortoise moves from $C$ to $B$ , moment of inertia increases. Therefore, angular velocity decreases

If, $M$ =mass of platform
$R=$ radius of platform
$m=$ mass of tortoise moving along the chord $AB$
$a=$ perpendicular distance of $O$ from $AB$
Initial angular momentum, $I_{1}=mR^{2}+\frac{M R^{2}}{2}$
At any time $t$ , let the tortoise reach $D$ moving with velocity $v$
$\therefore \, AD=vt$
$AC=\sqrt{R^{2} - a^{2}}$
As $DC=AC-AD=\left(\right.\sqrt{R^{2} - a^{2}}-vt\left.\right)$
$\therefore \, \, OD=r=a^{2}+\left[\sqrt{R^{2} - a^{2}} - v t\right]^{2}$
Angular momentum at time $t$
$I_{2}=mr^{2}+\frac{M R^{2}}{2}$
As angular momentum is conserved
$\therefore \quad I_1 \omega_0=I_2 \omega(t)$
This shows that variation of $\omega \left(\right.t\left.\right)$ with time is nonlinear. Choice