Q.
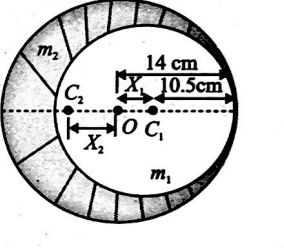
A circular plate of uniform thickness has a diameter of $28\,cm$. A circular portion of diameter $21 \,cm$ is removed from the plate as shown. $O$ is the centre of mass of complete plate. The position of centre of mass of remaining portion will shift towards left from $O$ by
System of Particles and Rotational Motion
Solution:
$C_{1}$ is the centre of mass of cut portion and $C_{2}$ that of remaining portion. We have to find $x_{2}$.
$ x_{1}=14-10.5=3.5\, cm$
Mass will be proportional to area. So
mass of the whole disc is
$M=k \pi(14)^{2}$
Mass of cut portion $m_{1}=k \pi(10.5)^{2}$
Mass of the remaining portion $m_{2}=$
$M-m_{1}=k \pi\left(14^{2}-10.5^{2}\right)=k \pi(24.5)$
$\times(3.5)$
Now, $m_{1} x_{1}=m_{2} x_{2}$
$\Rightarrow x_{2}=\frac{m_{1} x_{1}}{m_{2}}=\frac{k \pi(10.5)^{2} \times 3.5}{k \pi(24.5) \times 3.5}=4.5\, cm$