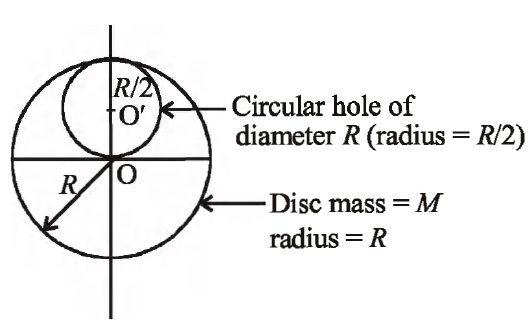
Q. A circular hole of diameter $R$ is cut from a disc of mass $M$ and radius $R$; the circumference of the cut passes through the centre of the disc. The moment of inertia of the remaining portion of the disc about an axis perpendicular to the disc and passing through its centre is
AIEEEAIEEE 2012System of Particles and Rotational Motion
Solution:
M.I. of complete disc about its centre $O$.
$I_{Total}=\frac{1}{2}MR^{2} \, ...\left(i\right)$
Mass of circular hole $\left(removed\right)$
$=\frac{M}{4}\left(As\,M=\pi R^{2}\,t \therefore M\,\propto\,R^{2}\right)$
M.I. of removed hole about its own axis
$=\frac{1}{2}\left(\frac{M}{4}\right)\left(\frac{R}{2}\right)^{2}=\frac{1}{32} \,MR^{2}$
$M.I.$ of removed hole about $O'$
$I_{removed hole }=I_{cm}+mx^{2}$
$=\frac{MR^{2}}{32}+\frac{M}{4}\left(\frac{R}{2}\right)^{2}$
$=\frac{MR^{2}}{32}+\frac{MR^{2}}{16}=\frac{3MR^{2}}{32}$
$M.I.$ of complete disc can also be written as
$I_{Total}=I_{removed hole}+I_{remaining disc}$
$I_{Total}=\frac{3MR^{2}}{32}+I_{remaining disc}\, ...\left(ii\right)$
From eq. $\left(i\right)$ and $\left(ii\right),$
$\frac{1}{2}MR^{2}=\frac{3MR^{2}}{32}+I_{remaining disc}$
$\Rightarrow I_{remaining disc}$
$=\frac{MR^{2}}{2}-\frac{3MR^{2}}{32}=\left(\frac{13}{32}\right)MR^{2}$